How to Create a Square Matrix from a Column Vector in Python

When working with numerical data in Python, you’ll often find yourself in situations where you must manipulate matrices. One such operation involves converting a column vector into a square matrix. But how do you do this? In this article, we’ll explore various methods to create a square matrix from a column vector so that you can choose what works best for your specific needs.

What is a Column Vector, and Why Do You Need to Convert It into a Square Matrix?

A column vector is a matrix with a single column like this:

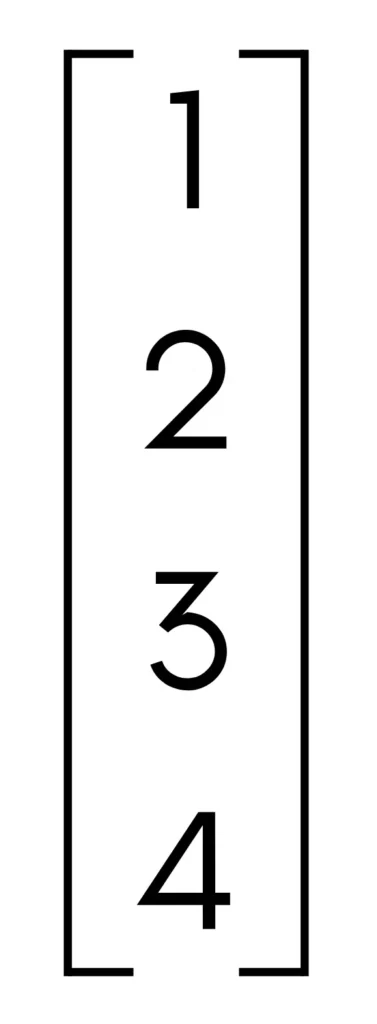
However, a square matrix has the same number of rows and columns. For instance, converting the above column vector into a 2×2 square matrix could look like this:

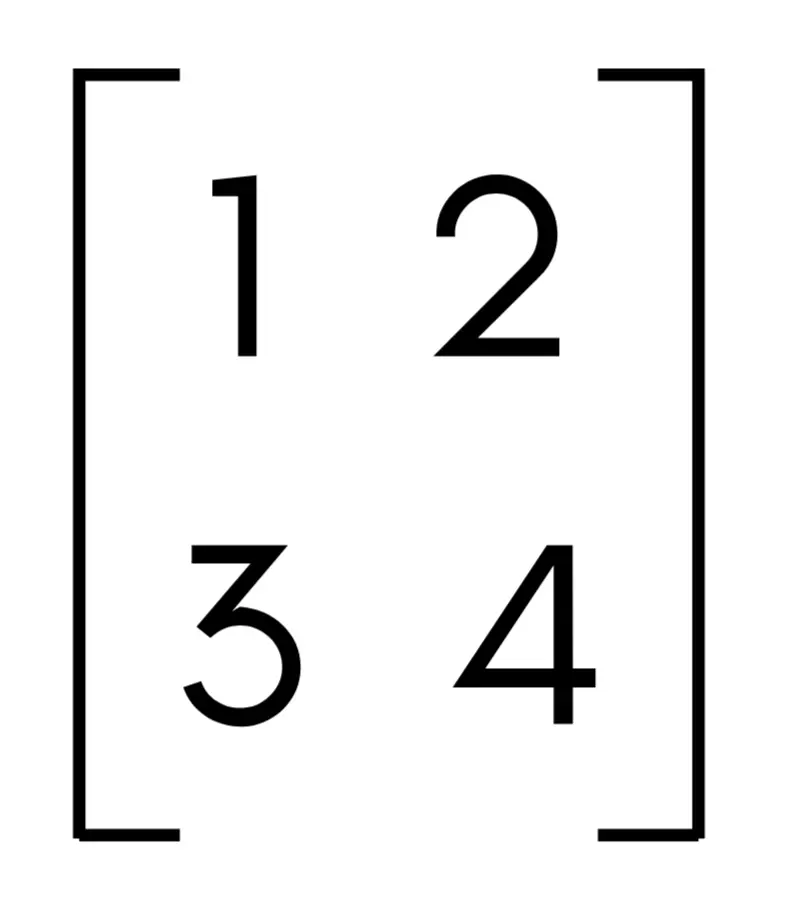
You might need to transform a column vector into a square matrix:

• To reshape data for machine learning algorithms.
• To structure data for mathematical operations.
• To prepare input for image processing and signal processing tasks.

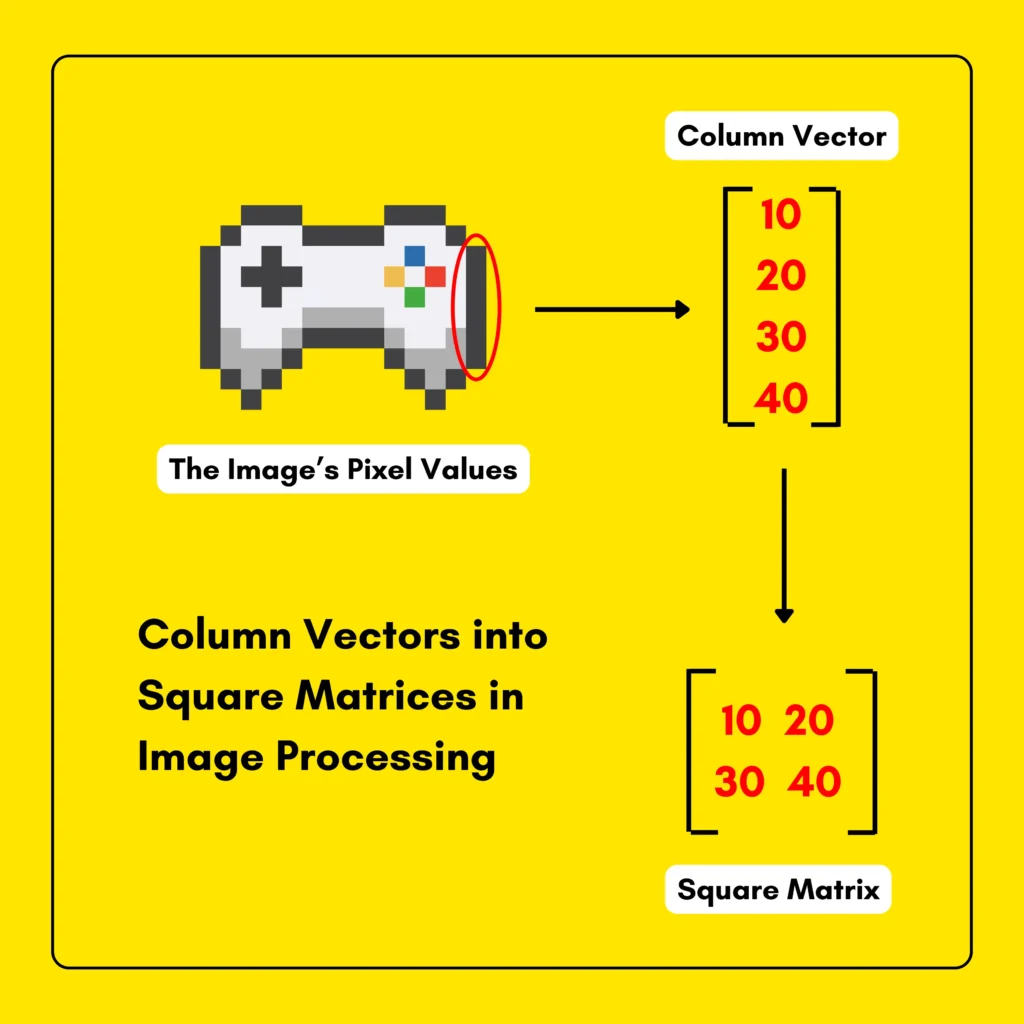
4 Easy Methods to Create a Square Matrix from a Column Vector

Method 1: Using Numpy’s reshape() Function

NumPy is the go-to library for all numerical operations in Python. You can use its reshape () function to convert a column vector into a square matrix. It’s quick and requires minimal code.

Example Code

• In this example, we first import the numpy library.
• Next, we create a 1D array called column_vector using np.array().
• The reshape(2,2) converts the array into a 2×2 square matrix.
• Finally, we print the matrix.

import numpy as np

# Define a column vector
column_vector = np.array([1, 2, 3, 4])

# Convert to a square matrix
square_matrix = column_vector.reshape(2, 2)

print(square_matrix)

Output

[[1 2]
 [3 4]]

Method 2: Using Numpy’s np.outer() Function

If you want a square matrix in which each element is the product of the corresponding element from the column vector, Numpy’s np.outer() function can do that job easily.

Example Code

• First, we create a 1D array using np.array()called column_vector.
• Then, np.outer(column_vector, column_vector) computes the outer product of the column vector, creating a square matrix where each element is the product of two elements from it.
• Finally, we print out the resulting square matrix.

import numpy as np

# Column vector
column_vector = np.array([1, 2, 3, 4])

# Convert to square matrix
square_matrix = np.outer(column_vector, column_vector)

print(square_matrix)

Output

[[ 1  2  3  4]
 [ 2  4  6  8]
 [ 3  6  9 12]
 [ 4  8 12 16]]

Method 3: Using NumPy’s resize() Function

Unlike the reshape() function, which does not modify the original array, resize() modifies it in place. This means you don’t need to assign it to a new variable to transform the column vector into the square matrix.

Example Code

• Here, we initialize a 1D array called column_vector.
• The column_vector.resize(2,2) directly modifies the original array, changing its shape to a 2×2 matrix.
• We then print the resulting square matrix.

import numpy as np

column_vector = np.array([1, 2, 3, 4])
column_vector.resize(2, 2)

print(column_vector)

Output

[[1 2]
 [3 4]]

Method 4: Using Matrix Multiplication

The multiplication of matrices is a key concept in linear algebra. By using matrix multiplication, you can create a square matrix and gain a deeper understanding of matrix operations.

Example Code

• In this example, a 1D array column_vector is defined first.
• Then, we use the np.dot() function to perform matrix multiplication between the column and row vectors.
• The column_vector[:, None] and column_vector[None, :] convert the 1D array into a column and a row vector, respectively.
• Lastly, we print the resulting square matrix.

import numpy as np

# Column vector
column_vector = np.array([1, 2, 3])

# Create a square matrix by multiplying the column vector with its transpose
square_matrix = np.dot(column_vector[:, None], column_vector[None, :])

print(square_matrix)

Output

[[1 2 3]
 [2 4 6]
 [3 6 9]]

What If the Column Vector Has Extra Elements?

Sometimes, the number of elements in a vector is not a perfect square. You can handle this situation in a few different ways:

1. Trim Extra Elements: Discard the extra elements to adjust the matrix to the closest possible square size.
2. Add Padding: Pad the vector with zeros (or another placeholder value) to make it fit a perfect square.

Example Code

• Here, we have a column vector with 5 elements in it.
• The variable n is calculated as the largest integer square root of the number of elements using int(np.sqrt(len(column_vector))).
• We then use slicing to discard the extra element (in this case, the number 5) and create a square matrix.
• Finally, the reshape() function transforms the adjusted vector into a square matrix.

import numpy as np

column_vector = np.array([1, 2, 3, 4, 5])
n = int(np.sqrt(len(column_vector)))  # Find the closest square size

# Trim extra elements to create a square matrix
square_matrix = column_vector[:n**2].reshape(n, n)
print(square_matrix)

Output

[[1 2]
 [3 4]]

Conclusion

In this article, we explored multiple ways to create a square matrix from a column vector in Python, each with its own advantages. Here’s a quick recap of the methods covered:

• Use reshape() for a quick and efficient solution.
• Use resize() if you want an in-place transformation.
• Use np.outer() to create a square matrix using element-wise multiplication.
• Use matrix multiplication (np.dot()) to form a structured square matrix.

Moreover, we’ve also seen how to handle cases when the column vector has extra elements, with options like trimming the vector or adding padding.

Now you can confidently choose the method that best fits your project.

For more Python tutorials, check out the Python Series on Syntax Scenarios and level up your coding skills!